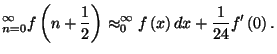Next: About this document ...
Chapter 9 - Answers to selected exercises
1. What is the compressibility of a gas of free fermions at zero
temperature? Obtain the numerical value for electrons with the density of
conduction electrons in metallic sodium. Compare your results with
experimental data for sodium at room temperature.
2. An ideal gas of fermions, with mass  and Fermi energy
and Fermi energy
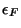 ,
is at rest at zero temperature. Find expressions for the expected values
,
is at rest at zero temperature. Find expressions for the expected values
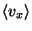 and
and
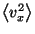 , where
, where 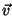 is the velocity of a fermion.
is the velocity of a fermion.
3. Consider a gas of free electrons, in a 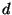 -dimensional space, within a
hypercubic container of side
-dimensional space, within a
hypercubic container of side 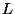 . Sketch graphs of the density of states
. Sketch graphs of the density of states
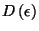 versus energy
versus energy 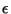 for dimensions
for dimensions 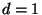 and
and 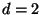 . What is the expression of the Fermi energy in terms of the
particle density for
. What is the expression of the Fermi energy in terms of the
particle density for 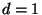 and
and 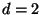 ?
?
4. Show that the chemical potential of an ideal classical gas of  monatomic particles, in a container of volume
monatomic particles, in a container of volume  , at temperature
, at temperature  , may
be written as
, may
be written as
where 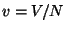 is the volume per particle, and
is the volume per particle, and
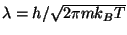 is the thermal wavelength. Sketch a graph of
is the thermal wavelength. Sketch a graph of
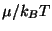 versus
versus  .
Obtain the first quantum correction to this result. That is, show that the
chemical potential of the ideal quantum gas may be written as the expansion
.
Obtain the first quantum correction to this result. That is, show that the
chemical potential of the ideal quantum gas may be written as the expansion
and obtain explicit expressions for the prefactor  for fermions and
bosons. Sketch a graph of
for fermions and
bosons. Sketch a graph of
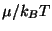 versus
versus
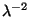 (that is,
versus the temperature in convenient units) for fermions, bosons, and
classical particles.
(that is,
versus the temperature in convenient units) for fermions, bosons, and
classical particles.
5. Obtain an asymptotic form, in the limit  , for the specific heat
of a gas of
, for the specific heat
of a gas of  free fermions adsorbed on a surface of area
free fermions adsorbed on a surface of area  , at a given
temperature
, at a given
temperature  .
.
6. Consider a gas of  free electrons, in a region of volume
free electrons, in a region of volume  , in the
ultrarelativistic regime. The energy spectrum is given by
, in the
ultrarelativistic regime. The energy spectrum is given by
where 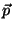 is the linear momentum.
(a) Calculate the Fermi energy of this system.
(b) What is the total energy in the ground state?
(c) Obtain an asymptotic form for the specific heat at constant volume in
the limit
is the linear momentum.
(a) Calculate the Fermi energy of this system.
(b) What is the total energy in the ground state?
(c) Obtain an asymptotic form for the specific heat at constant volume in
the limit  .
.
7. At low temperatures, the internal energy of a system of free electrons
may be written as an expansion,
Obtain the value of the constant  , and indicate the order of magnitude of
the terms that have been discarded.
, and indicate the order of magnitude of
the terms that have been discarded.
8. Consider a system of free fermions in 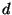 dimensions, with the energy
spectrum
dimensions, with the energy
spectrum
where 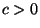 and
and 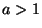 .
(a) Calculate the prefactor
.
(a) Calculate the prefactor  of the relation
of the relation  .
(b) Calculate the Fermi energy as a function of volume
.
(b) Calculate the Fermi energy as a function of volume  and number of
particles
and number of
particles  .
(c) Calculate an asymptotic expression, in the limit
.
(c) Calculate an asymptotic expression, in the limit  , for the
specific heat at constant volume.
, for the
specific heat at constant volume.
9. Consider again the gas of  ultrarelativistic free electrons, within a
container of volume
ultrarelativistic free electrons, within a
container of volume  , at temperature
, at temperature  , in the presence of a magnetic
field
, in the presence of a magnetic
field 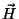 . If we neglect the effects of orbital magnetism, the energy
spectrum is given by
. If we neglect the effects of orbital magnetism, the energy
spectrum is given by
where  is the Bohr magneton and
is the Bohr magneton and
 .
(a) Show that the Fermi energy of this system may be written as
.
(a) Show that the Fermi energy of this system may be written as
Obtain expressions for the prefactors  and
and 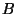 .
(b) Show that the magnetization in the ground state can be written in the
form
.
(b) Show that the magnetization in the ground state can be written in the
form
Obtain an expression for the constant  .
(c) Calculate the susceptibility of the ground state in zero field.
.
(c) Calculate the susceptibility of the ground state in zero field.
10. In the classical paramagnetic theory of Langevin, proposed before the
advent of quantum statistics, we assume a classical Hamiltonian, given by
where
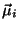 is the magnetic moment of a localized ion.
(a) Show that the canonical partition function of this system is given by
is the magnetic moment of a localized ion.
(a) Show that the canonical partition function of this system is given by
where  is the elementary solid angle of integration.
(b) Show that the magnetization (along the direction of the field) is given
by
is the elementary solid angle of integration.
(b) Show that the magnetization (along the direction of the field) is given
by
where
is the Langevin function.
(c) Show that the susceptibility in zero field is given by the Curie law,
11. Obtain an expression for the magnetic susceptibility associated with the
orbital motion of free electrons in the presence of a uniform magnetic field
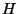 , under conditions of strong degeneracy,
, under conditions of strong degeneracy,  , and very weak
fields,
, and very weak
fields,
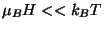 . To simplify the expression of
. To simplify the expression of  , you may
use Euler's sum rule,
, you may
use Euler's sum rule,



Next: About this document ...
Jairo da Silva
2001-03-12
![]() and Fermi energy
and Fermi energy
![]() ,
is at rest at zero temperature. Find expressions for the expected values
,
is at rest at zero temperature. Find expressions for the expected values
![]() and
and
![]() , where
, where ![]() is the velocity of a fermion.
is the velocity of a fermion.
![]() -dimensional space, within a
hypercubic container of side
-dimensional space, within a
hypercubic container of side ![]() . Sketch graphs of the density of states
. Sketch graphs of the density of states
![]() versus energy
versus energy ![]() for dimensions
for dimensions ![]() and
and ![]() . What is the expression of the Fermi energy in terms of the
particle density for
. What is the expression of the Fermi energy in terms of the
particle density for ![]() and
and ![]() ?
?
![]() monatomic particles, in a container of volume
monatomic particles, in a container of volume ![]() , at temperature
, at temperature ![]() , may
be written as
, may
be written as
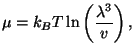
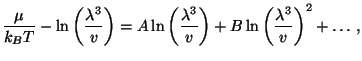
![]() , for the specific heat
of a gas of
, for the specific heat
of a gas of ![]() free fermions adsorbed on a surface of area
free fermions adsorbed on a surface of area ![]() , at a given
temperature
, at a given
temperature ![]() .
.
![]() free electrons, in a region of volume
free electrons, in a region of volume ![]() , in the
ultrarelativistic regime. The energy spectrum is given by
, in the
ultrarelativistic regime. The energy spectrum is given by
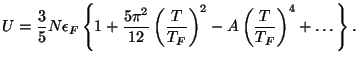
![]() dimensions, with the energy
spectrum
dimensions, with the energy
spectrum
![]() ultrarelativistic free electrons, within a
container of volume
ultrarelativistic free electrons, within a
container of volume ![]() , at temperature
, at temperature ![]() , in the presence of a magnetic
field
, in the presence of a magnetic
field ![]() . If we neglect the effects of orbital magnetism, the energy
spectrum is given by
. If we neglect the effects of orbital magnetism, the energy
spectrum is given by
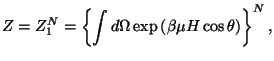
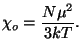
![]() , under conditions of strong degeneracy,
, under conditions of strong degeneracy, ![]() , and very weak
fields,
, and very weak
fields,
![]() . To simplify the expression of
. To simplify the expression of ![]() , you may
use Euler's sum rule,
, you may
use Euler's sum rule,