


Next: About this document ...
Chapter 3- Answers to selected exercises
1. The chemical potential of a simple fluid of a single component is given
by the expression
where 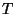 is the temperature,
is the temperature,  is the pressure,
is the pressure, 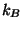 is the Boltzmann
constant, and the functions
is the Boltzmann
constant, and the functions
 and
and
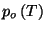 are well behaved. Show that this system obeys Boyle's law,
are well behaved. Show that this system obeys Boyle's law,
 . Obtain an expression for the specific heat at constant
pressure. What are the expressions for the thermal compressibility, the
specific heat at constant volume, and the thermal expansion coefficient?
Obtain the density of Helmholtz free energy,
. Obtain an expression for the specific heat at constant
pressure. What are the expressions for the thermal compressibility, the
specific heat at constant volume, and the thermal expansion coefficient?
Obtain the density of Helmholtz free energy,
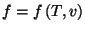 .
Hint: Note that
.
Hint: Note that
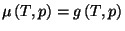 . Thus
. Thus
which is the expression of Boyle's law, and
from which we obtain the specific heat at constant pressure. All other
expressions are straightforward. In particular,
2. Consider a pure fluid of one component. Show that
Use this result to show that the specific heat of an ideal gas does not
depend on volume. Show that
3. Consider a pure fluid characterized by the grand thermodynamic potential
where
 is a well-behaved function. Write the
equations of state in this thermodynamic representation. Obtain an
expression for the internal energy as a function of
is a well-behaved function. Write the
equations of state in this thermodynamic representation. Obtain an
expression for the internal energy as a function of 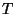 ,
, 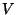 , and
, and 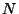 .
Obtain an expression for the Helmholtz free energy of this system. Calculate
the thermodynamic derivatives
.
Obtain an expression for the Helmholtz free energy of this system. Calculate
the thermodynamic derivatives
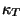 and
and 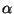 as a function of
temperature and pressure.
From Euler's relation, we have
as a function of
temperature and pressure.
From Euler's relation, we have
Thus, we can write
which is identical to the expression for the chemical potential in exercise
1, if we make
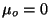 and
and
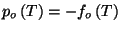 . Therefore, we have Boyle's law and the usual expressions for
. Therefore, we have Boyle's law and the usual expressions for
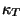 and
and 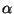 .
.
4. Obtain an expression for the Helmholtz free energy per particle,
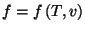 , of a pure system given by the equations of state
, of a pure system given by the equations of state
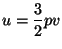 and and 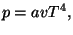 |
|
where 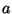 is a constant.
Note that we can write the following equations of state in the entropy
representation
is a constant.
Note that we can write the following equations of state in the entropy
representation
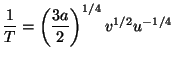 and
and 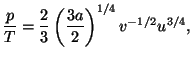 |
|
that lead to the fundamental equation
where 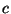 is a constant. The Helmholtz free energy is given by
is a constant. The Helmholtz free energy is given by
5. Obtain an expression for the Gibbs free energy per particle,
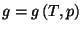 , for a pure system given by the fundamental equation
, for a pure system given by the fundamental equation
where 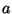 and
and 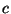 are constants.
From the fundamental equation
are constants.
From the fundamental equation
we write the equations of state
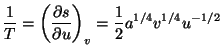 and and  |
|
The Gibbs free energy per particle is given by the Legendre transformation
where  and
and  come from the equations of state.
come from the equations of state.
6. Consider an elastic ribbon of length  under a tension
under a tension  . In a
quasi-static process, we can write
. In a
quasi-static process, we can write
Suppose that the tension is increased very quickly, from  to
to
 , keeping the temperature
, keeping the temperature 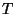 fixed. Obtain an expression for the change of
entropy just after reaching equilibrium. What is the change of entropy per
mole for an elastic ribbon that behaves according to the equation of state
fixed. Obtain an expression for the change of
entropy just after reaching equilibrium. What is the change of entropy per
mole for an elastic ribbon that behaves according to the equation of state 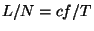 , where
, where 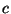 is a constant?
Using the Gibbs representation, we have the Maxwell relation
is a constant?
Using the Gibbs representation, we have the Maxwell relation
The equation of state, 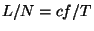 , leads to the result
, leads to the result
7. A magnetic compound behaves according to the Curie law, 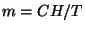 , where
, where  is a constant,
is a constant, 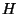 is the applied magnetic field,
is the applied magnetic field, 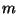 is the
magnetization per particle (with corrections due to presumed surface
effects), and
is the
magnetization per particle (with corrections due to presumed surface
effects), and 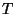 is temperature. In a quasi-static process, we have
is temperature. In a quasi-static process, we have
where
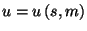 plays the role of an internal energy. For an
infinitesimal adiabatic process, show that we can write
plays the role of an internal energy. For an
infinitesimal adiabatic process, show that we can write
where  is the specific heat at constant magnetic field.
is the specific heat at constant magnetic field.
8. From stability arguments, show that the enthalpy of a pure fluid is a
convex function of entropy and a concave function of pressure.
*9. Show that the entropy per mole of a pure fluid,
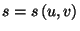 , is a concave function of its variables. Note that we have to
analyze the sign of the quadratic form
, is a concave function of its variables. Note that we have to
analyze the sign of the quadratic form
This quadratic form can be written in the matrix notation
The eigenvalues of the  matrix are the roots of the quadratic
equation
matrix are the roots of the quadratic
equation
For a concave function, the eigenvalues are negative, that is,
and
Now it is straightforward to relate these derivatives of the entropy with
positive physical quantities (as the compressibilities and the specific
heats).



Next: About this document ...
Jairo da Silva
2001-03-12

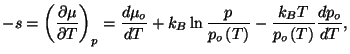
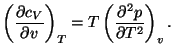
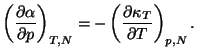
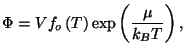
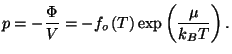
![]() , of a pure system given by the equations of state
, of a pure system given by the equations of state
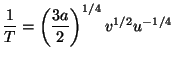 and
and 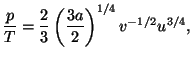
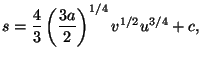
![$\displaystyle f\left( T,v\right) =u-Ts=\frac{3a}{2}v^{2}T^{4}-T\left[ \frac{4}{...
...{2}\right) ^{1/4}v^{1/2}\left( \frac{3a}{2}v^{2}T^{4}\right)
^{3/4}+c\right] .$](img32.gif)
![]() , for a pure system given by the fundamental equation
, for a pure system given by the fundamental equation
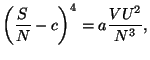
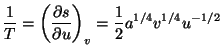 and
and 
![]() under a tension
under a tension ![]() . In a
quasi-static process, we can write
. In a
quasi-static process, we can write


![]() , where
, where ![]() is a constant,
is a constant, ![]() is the applied magnetic field,
is the applied magnetic field, ![]() is the
magnetization per particle (with corrections due to presumed surface
effects), and
is the
magnetization per particle (with corrections due to presumed surface
effects), and ![]() is temperature. In a quasi-static process, we have
is temperature. In a quasi-static process, we have
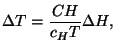
![]() , is a concave function of its variables. Note that we have to
analyze the sign of the quadratic form
, is a concave function of its variables. Note that we have to
analyze the sign of the quadratic form
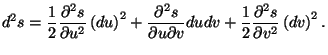
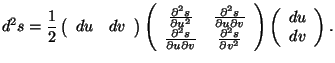
![$\displaystyle \lambda ^{2}-\left[ \frac{\partial ^{2}s}{\partial u^{2}}+\frac{\...
...rtial v^{2}}-\left[ \frac{\partial ^{2}s}{\partial
u\partial v}\right] ^{2}=0.$](img60.gif)
![$\displaystyle \frac{\partial ^{2}s}{\partial u^{2}}\frac{\partial ^{2}s}{\partial v^{2}}-
\left[ \frac{\partial ^{2}s}{\partial u\partial v}\right] ^{2}>0$](img61.gif)
