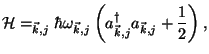Next: About this document ...
Chapter 10 - Answers to selected exercises
1. Consider a system of ideal bosons of zero spin ( ), within a
container of volume
), within a
container of volume  .
(a) Show that the entropy above the condensation temperature
.
(a) Show that the entropy above the condensation temperature  is
given by
is
given by
where
and
(b) Given  and
and  , what is the expression of the entropy below
, what is the expression of the entropy below  ?
What is the entropy associated with the particles of the condensate?
(c) From the expression for the entropy, show that the specific heat at
constant volume above
?
What is the entropy associated with the particles of the condensate?
(c) From the expression for the entropy, show that the specific heat at
constant volume above 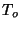 is given by
is given by
(d) Below 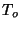 , show that the specific heat at constant volume is given
by
, show that the specific heat at constant volume is given
by
(e) Given the specific volume  , sketch a graph of
, sketch a graph of
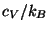 versus
versus
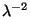 (that is, in terms of the temperature in convenient units).
Obtain the asymptotic expressions of the specific heat for
(that is, in terms of the temperature in convenient units).
Obtain the asymptotic expressions of the specific heat for
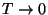 and
and
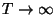 . Obtain the value of the specific heat at
. Obtain the value of the specific heat at 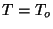 .
.
2. Consider again the same problem for an ideal gas of two-dimensional
bosons confined to a surface of area 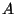 . What are the changes in the
expressions of item (a)? Show that there is no Bose-Einstein condensation
in two dimensions (that is, show that in this case the Bose-Einstein
temperature vanishes).
. What are the changes in the
expressions of item (a)? Show that there is no Bose-Einstein condensation
in two dimensions (that is, show that in this case the Bose-Einstein
temperature vanishes).
3. Consider an ideal gas of bosons with internal degrees of freedom. Suppose
that, besides the ground state with zero energy (
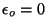 ), we have
to take into account the first excited state, with internal energy
), we have
to take into account the first excited state, with internal energy
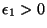 . In other words, assume that the energy spectrum is given by
. In other words, assume that the energy spectrum is given by
where
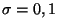 . Obtain an expression for the Bose-Einstein
condensation temperature as a function of the parameter
. Obtain an expression for the Bose-Einstein
condensation temperature as a function of the parameter
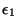 .
.
4. Consider a gas of non-interacting bosons associated with the energy
spectrum
where 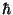 and
and 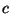 are constants, and
are constants, and 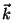 is a wave vector.
Calculate the pressure of this gas at zero chemical potential. What is the
pressure of radiation of a gas of photons?
is a wave vector.
Calculate the pressure of this gas at zero chemical potential. What is the
pressure of radiation of a gas of photons?
*5. The Hamiltonian of a gas of photons within an empty cavity of volume  is given by the expression
is given by the expression
where 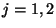 indicates the polarization,
indicates the polarization, 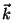 is the wave vector,
is the wave vector,
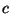 is the velocity of light, and
is the velocity of light, and
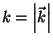 .
(a) Use the formalism of the occupation numbers (second quantization) to
obtain the canonical partition function associated with this system.
(b) Show that the internal energy is given by
.
(a) Use the formalism of the occupation numbers (second quantization) to
obtain the canonical partition function associated with this system.
(b) Show that the internal energy is given by
Obtain the value of the constants 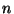 and
and 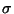 .
(c) Consider the Sun as a black body at temperature
.
(c) Consider the Sun as a black body at temperature
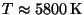 . The solar diameter and the distance between the Sun and the Earth are of
the order of
. The solar diameter and the distance between the Sun and the Earth are of
the order of
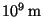 and
and
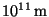 , respectively.
Obtain the intensity of the total radiation that reaches the surface of
Earth. What is the value of the pressure of this radiation?
, respectively.
Obtain the intensity of the total radiation that reaches the surface of
Earth. What is the value of the pressure of this radiation?



Next: About this document ...
Jairo da Silva
2001-03-12
![$\displaystyle S=k_{B}\frac{V}{\lambda ^{3}}\left[ \frac{5}{2}g_{5/2}\left( z\right) -\frac{
\mu }{k_{B}T}g_{3/2}\left( z\right) \right] ,$](img4.gif)
![$\displaystyle S=k_{B}\frac{V}{\lambda ^{3}}\left[ \frac{5}{2}g_{5/2}\left( z\right) -\frac{
\mu }{k_{B}T}g_{3/2}\left( z\right) \right] ,$](img4.gif)
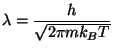

![$\displaystyle c_{V}=\frac{3}{4}k_{B}\left[ 5\frac{g_{5/2}\left( z\right) }{g_{3...
...(
z\right) }-3\frac{g_{3/2}\left( z\right) }{g_{1/2}\left( z\right) }\right] .$](img8.gif)
![]() . What are the changes in the
expressions of item (a)? Show that there is no Bose-Einstein condensation
in two dimensions (that is, show that in this case the Bose-Einstein
temperature vanishes).
. What are the changes in the
expressions of item (a)? Show that there is no Bose-Einstein condensation
in two dimensions (that is, show that in this case the Bose-Einstein
temperature vanishes).
![]() ), we have
to take into account the first excited state, with internal energy
), we have
to take into account the first excited state, with internal energy
![]() . In other words, assume that the energy spectrum is given by
. In other words, assume that the energy spectrum is given by
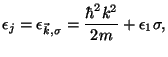
![]() is given by the expression
is given by the expression