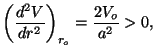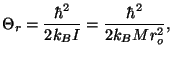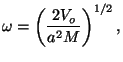Next: About this document ...
Chapter 8- Answers to selected exercises
1. Obtain the explicit forms of the ground state and of the first excited
state for a system of two free bosons, with zero spin, confined to a
one-dimensional region of length  . Repeat this problem for two fermions
of spin
. Repeat this problem for two fermions
of spin 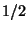 .
The single-particle states are given by
.
The single-particle states are given by
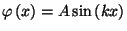 , where
, where
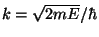 and
and 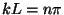 , with
, with
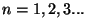 . Note that
. Note that
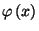 vanishes at
vanishes at 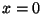 and
and 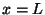 .
The ground state is given by
.
The ground state is given by
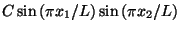 , where
, where 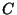 is a normalization constant.
The first excited state is given by
is a normalization constant.
The first excited state is given by
2. Show that the entropy of an ideal quantum gas may be written as
where the upper (lower) sign refers to fermions (bosons), and
is the Fermi-Dirac (Bose-Einstein) distribution. Show that we can still
use these equations to obtain the usual results for the classical ideal
gas.
3. Show that the equation of state
holds for both free bosons and fermions (and also in the classical case).
Show that an ideal ultrarelativistic gas, given by the energy spectrum
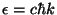 , still obeys the same equation of state.
For fermions, we have
, still obeys the same equation of state.
For fermions, we have
In the thermodynamic limit, for free fermions, we can write
from which we prove that 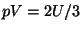 . The same manipulations can be carried
out for bosons, but we should pay special attention to the
. The same manipulations can be carried
out for bosons, but we should pay special attention to the 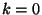 state. For
the classical gas, this result is trivial.
state. For
the classical gas, this result is trivial.
4. Consider a quantum ideal gas inside a cubic vessel of side  , and
suppose that the orbitals of the particles are associated with wave
functions that vanish at the surfaces of the cube. Find the density of
states in
, and
suppose that the orbitals of the particles are associated with wave
functions that vanish at the surfaces of the cube. Find the density of
states in 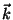 space. In the thermodynamic limit, show that we have the
same expressions as calculated with periodic boundary conditions.
space. In the thermodynamic limit, show that we have the
same expressions as calculated with periodic boundary conditions.
5. An ideal gas of 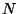 atoms of mass
atoms of mass 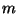 is confined to a vessel of volume
is confined to a vessel of volume 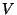 , at a given temperature
, at a given temperature 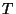 . Calculate the classical limit of the
chemical potential of this gas.
Now consider a ``two-dimensional'' gas of
. Calculate the classical limit of the
chemical potential of this gas.
Now consider a ``two-dimensional'' gas of 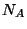 free particles adsorbed on
a surface of area
free particles adsorbed on
a surface of area 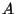 . The energy of an adsorbed particle is given by
. The energy of an adsorbed particle is given by
where 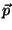 is the (two-dimensional) momentum, and
is the (two-dimensional) momentum, and
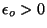 is
the binding energy that keeps the particle stuck to the surface. In the
classical limit, calculate the chemical potential
is
the binding energy that keeps the particle stuck to the surface. In the
classical limit, calculate the chemical potential  of the adsorbed
gas.
The condition of equilibrium between the adsorbed particles and the
particles of the three-dimensional gas can be expressed in terms of the
respective chemical potentials. Use this condition to find the surface
density of adsorbed particles as a function of temperature and pressure
of the adsorbed
gas.
The condition of equilibrium between the adsorbed particles and the
particles of the three-dimensional gas can be expressed in terms of the
respective chemical potentials. Use this condition to find the surface
density of adsorbed particles as a function of temperature and pressure 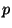 of the surrounding gas.
In the thermodynamic limit, the chemical potential of the three-dimensional
gas is given by
of the surrounding gas.
In the thermodynamic limit, the chemical potential of the three-dimensional
gas is given by
For the adsorbed gas, we have the classical limit
which yields the chemical potential
From the physical requirement of equilibrium,
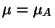 , we obtain
, we obtain  in terms of temperature and pressure.
in terms of temperature and pressure.
6. Obtain an expression for the entropy per particle, in terms of
temperature and density, for a classical ideal monatomic gas of 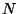 particles of spin
particles of spin 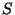 adsorbed on a surface of area
adsorbed on a surface of area 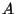 . Obtain the expected
values of
. Obtain the expected
values of
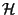 ,
,
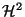 ,
,
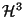 , where
, where
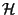 is the Hamiltonian of the system. What are the expressions of
the second and third moments of the Hamiltonian with respect to its average
value?
is the Hamiltonian of the system. What are the expressions of
the second and third moments of the Hamiltonian with respect to its average
value?
7. Consider a homogeneous mixture of two ideal monatomic gases, at
temperature 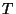 , inside a container of volume
, inside a container of volume 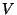 . Suppose that there are
. Suppose that there are 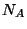 particles of gas
particles of gas 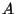 and
and 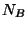 particles of gas
particles of gas 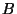 . Write an
expression for the grand partition function associated with this system (it
should depend on
. Write an
expression for the grand partition function associated with this system (it
should depend on 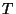 ,
, 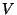 , and the chemical potentials
, and the chemical potentials  and
and  ). In the classical limit, obtain expressions for the canonical
partition function, the Helmholtz free energy
). In the classical limit, obtain expressions for the canonical
partition function, the Helmholtz free energy 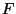 , and the pressure
, and the pressure 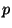 of
the gas. Show that
of
the gas. Show that
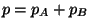 (Dalton's law), where
(Dalton's law), where 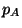 and
and  are the partial pressures of
are the partial pressures of 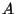 and
and 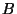 , respectively.
, respectively.
8. Under some conditions, the amplitudes of vibration of a diatomic molecule
may be very large, with a certain degree of anharmonicity. In this case, the
vibrational energy levels are given by the approximate expression
where  is the parameter of anharmonicity. To first order in
is the parameter of anharmonicity. To first order in  , obtain
an expression for the vibrational specific heat of this system.
Note that
, obtain
an expression for the vibrational specific heat of this system.
Note that
where
with
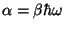 . We then have
. We then have
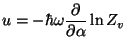 and
and  |
|
from which we calculate the first-order correction to the specific heat,
9. The potential energy between atoms of a hydrogen molecule may be
described by the Morse potential,
where
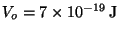 ,
,
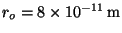 , and
, and
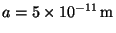 . Sketch a graph of
. Sketch a graph of
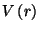 versus
versus 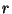 . Calculate the characteristic temperatures of
vibration and rotation to compare with experimental data (see table on
Section 8.4).
Note that
. Calculate the characteristic temperatures of
vibration and rotation to compare with experimental data (see table on
Section 8.4).
Note that
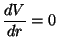 for for  |
|
and
which shows the existence of a minimum at  .
The characteristic temperature of rotation is given by
.
The characteristic temperature of rotation is given by
where  is the moment of inertia and
is the moment of inertia and 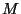 is the reduced mass of the
hydrogen molecule.
From the frequency of vibrations,
is the reduced mass of the
hydrogen molecule.
From the frequency of vibrations,
we write the characteristic temperature of vibrations,
Now it is easy to check the numerical predictions.



Next: About this document ...
Jairo da Silva
2001-03-12
![$\displaystyle \dsum\limits_{j}\ln \left[ 1+z\exp \left( -\beta \epsilon _{j}\ri...
...}dk\ln \left[ 1+z\exp \left( -\frac{\beta \hbar ^{2}k^{2}}{2m}\right)
\right]$](img18.gif)
![$\displaystyle =\frac{V\gamma }{\left( 2\pi \right) ^{3}}\left\{ \left. \frac{4\...
...-1}\exp
\left( \frac{\beta \hbar ^{2}k^{2}}{2m}\right) +1\right] ^{-1}\right\}$](img19.gif)

![]() , and
suppose that the orbitals of the particles are associated with wave
functions that vanish at the surfaces of the cube. Find the density of
states in
, and
suppose that the orbitals of the particles are associated with wave
functions that vanish at the surfaces of the cube. Find the density of
states in ![]() space. In the thermodynamic limit, show that we have the
same expressions as calculated with periodic boundary conditions.
space. In the thermodynamic limit, show that we have the
same expressions as calculated with periodic boundary conditions.
![]() atoms of mass
atoms of mass ![]() is confined to a vessel of volume
is confined to a vessel of volume ![]() , at a given temperature
, at a given temperature ![]() . Calculate the classical limit of the
chemical potential of this gas.
Now consider a ``two-dimensional'' gas of
. Calculate the classical limit of the
chemical potential of this gas.
Now consider a ``two-dimensional'' gas of ![]() free particles adsorbed on
a surface of area
free particles adsorbed on
a surface of area ![]() . The energy of an adsorbed particle is given by
. The energy of an adsorbed particle is given by
![$\displaystyle \mu =k_{B}T\ln \left[ \frac{8\pi ^{3}}{\gamma }\frac{N}{V}\left( \frac{\beta
\hbar ^{2}}{2\pi m}\right) ^{3/2}\right] .$](img35.gif)
![$\displaystyle \ln \Xi =\dsum\limits_{j}z\exp \left( -\beta \epsilon _{j}\right)...
...i k\exp \left[ -
\frac{\beta \hbar ^{2}k^{2}}{2m}+\beta \epsilon _{o}\right] ,$](img36.gif)
![$\displaystyle \mu _{A}=k_{B}T\ln \left[ \frac{4\pi ^{2}}{\gamma }\frac{N_{A}}{A}\left(
\frac{\beta \hbar ^{2}}{2\pi m}\right) \right] -\epsilon _{o}.$](img37.gif)
![]() particles of spin
particles of spin ![]() adsorbed on a surface of area
adsorbed on a surface of area ![]() . Obtain the expected
values of
. Obtain the expected
values of
![]() ,
,
![]() ,
,
![]() , where
, where
![]() is the Hamiltonian of the system. What are the expressions of
the second and third moments of the Hamiltonian with respect to its average
value?
is the Hamiltonian of the system. What are the expressions of
the second and third moments of the Hamiltonian with respect to its average
value?
![]() , inside a container of volume
, inside a container of volume ![]() . Suppose that there are
. Suppose that there are ![]() particles of gas
particles of gas ![]() and
and ![]() particles of gas
particles of gas ![]() . Write an
expression for the grand partition function associated with this system (it
should depend on
. Write an
expression for the grand partition function associated with this system (it
should depend on ![]() ,
, ![]() , and the chemical potentials
, and the chemical potentials ![]() and
and ![]() ). In the classical limit, obtain expressions for the canonical
partition function, the Helmholtz free energy
). In the classical limit, obtain expressions for the canonical
partition function, the Helmholtz free energy ![]() , and the pressure
, and the pressure ![]() of
the gas. Show that
of
the gas. Show that
![]() (Dalton's law), where
(Dalton's law), where ![]() and
and ![]() are the partial pressures of
are the partial pressures of ![]() and
and ![]() , respectively.
, respectively.
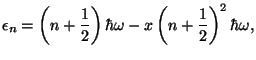

![$\displaystyle S\left( \alpha \right) =\dsum\limits_{n=0}^{\infty }\exp \left[ -...
...t( n+\frac{1}{2}\right) \right] =\left[ 2\sinh \frac{\alpha }{2}\right]
^{-1},$](img54.gif)
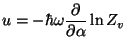 and
and 
![$\displaystyle \Delta c=k_{B}\left( \frac{\hbar \omega }{k_{B}T}\right) ^{2}x\fr...
...t( \alpha \right) }\frac{d^{2}}{
d\alpha ^{2}}S\left( \alpha \right) \right] .$](img58.gif)
![$\displaystyle V\left( r\right) =V_{o}\left\{ \exp \left[ -\frac{2\left( r-r_{o}\right) }{a}
\right] -2\exp \left[ -\frac{r-r_{o}}{a}\right] \right\} ,$](img59.gif)
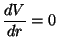 for
for