Next: About this document ...
Chapter 7- Answers to selected exercises
1. Show that the entropy in the grand canonical ensemble can be written as
with probability 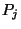 given by,
given by,
Show that this same form of entropy still holds in the pressure ensemble
(with a suitable probability distribution).
2. Consider a classical ultrarelativistic gas of particles, given by the
Hamiltonian
where 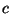 is a positive constant, inside a container of volume
is a positive constant, inside a container of volume 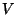 , in
contact with a reservoir of heat and particles (at temperature
, in
contact with a reservoir of heat and particles (at temperature 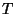 and
chemical potential
and
chemical potential 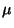 ). Obtain the grand partition function and the
grand thermodynamic potential. From a Legendre transformation of the grand
potential, write an expression for the Helmholtz free energy of this system.
To check your result, use the integral in equation (
). Obtain the grand partition function and the
grand thermodynamic potential. From a Legendre transformation of the grand
potential, write an expression for the Helmholtz free energy of this system.
To check your result, use the integral in equation (![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) ) for
obtaining an asymptotic form for the canonical partition function.
As we have already calculated in a previous exercise, the canonical
partition function is given by
) for
obtaining an asymptotic form for the canonical partition function.
As we have already calculated in a previous exercise, the canonical
partition function is given by
Using this expression, we obtain the grand canonical partition function,
from which we have the grand potential,
If we write
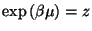 , the canonical partition
function is given by
, the canonical partition
function is given by
where
where 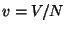 . From a saddle-point integration (see Appendix), we have
. From a saddle-point integration (see Appendix), we have
Now we should note that the same expression comes from the asymptotic form
3. Obtain the grand partition function of a classical system of particles,
inside a container of volume 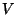 , given by the Hamiltonian
, given by the Hamiltonian
Write the equations of state in the representation of the grand potential.
For all reasonable forms of the single-particle potential
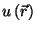 , show that the energy and the pressure obey typical equations of
an ideal gas.
, show that the energy and the pressure obey typical equations of
an ideal gas.
4. Show that the average quadratic deviation of the number of particles in
the grand canonical ensemble may be written as
Obtain an expression for the relative deviation
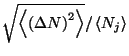 of an
ideal gas of classical monatomic particles.
For a classical ideal gas of monatomic particles, we have
of an
ideal gas of classical monatomic particles.
For a classical ideal gas of monatomic particles, we have
and
The relative deviation is thus of order
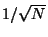 .
.
5. Show that the average quadratic deviation of energy in the grand
canonical ensemble may be written as
where
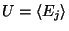 is the thermodynamic internal
energy in terms of
is the thermodynamic internal
energy in terms of 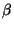 ,
, 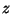 , and
, and 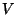 . Hence, show that we may also
write
. Hence, show that we may also
write
(you may use the Jacobian transformations of Appendix A.5). From this last
expression, show that
where
is the average quadratic deviation of energy in the canonical ensemble.
Finally, show that
since
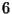 . At a given temperature
. At a given temperature 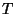 , a surface with
, a surface with 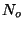 adsorption centers
has
adsorption centers
has
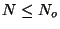 adsorbed molecules. Suppose that there are no interactions
between molecules. Show that the chemical potential of the adsorbed gas is
given by
adsorbed molecules. Suppose that there are no interactions
between molecules. Show that the chemical potential of the adsorbed gas is
given by
What is the meaning of the function
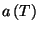 ?
Suppose an adsorbed particle has energy
?
Suppose an adsorbed particle has energy 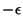 . We then write the
canonical partition function
. We then write the
canonical partition function
Now we can use the grand-canonical formalism to write
from which we have
and the expression for the chemical potential with
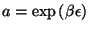 .
.
7. The grand partition function for a simplified statistical model is given
by the expression
where 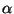 is a positive constant. Write parametric forms of the
equation of state. Sketch an isotherm of pressure versus specific volume
(draw a graph to eliminate the variable
is a positive constant. Write parametric forms of the
equation of state. Sketch an isotherm of pressure versus specific volume
(draw a graph to eliminate the variable 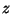 ). Show that this system displays
a (first-order) phase transition. Obtain the specific volumes of the
coexisting phases at this transition. Find the zeros of the polynomial
). Show that this system displays
a (first-order) phase transition. Obtain the specific volumes of the
coexisting phases at this transition. Find the zeros of the polynomial
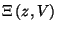 in the complex
in the complex 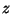 plane, and show that there is a zero
at
plane, and show that there is a zero
at 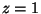 in the limit
in the limit
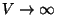 .
Note the structures of zeroes at
.
Note the structures of zeroes at 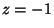 and
and
![$ z=\exp \left[ i\pi \left(
2n+1\right) /\left( \alpha V\right) \right] $](img54.gif) , for
, for
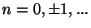 Also, note the thermodynamic limit,
Also, note the thermodynamic limit,
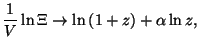 for for 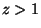 |
|
and
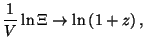 for for 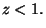 |
|
For 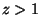 , we have the equations of state
, we have the equations of state
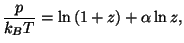 and and 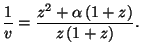 |
|
For 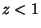 , we have
, we have
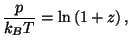 and and 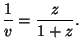 |
|
There is a first-order transition [
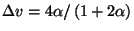 ] at
] at 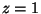 .
.



Next: About this document ...
Jairo da Silva
2001-03-12
![$\displaystyle Z_{N}=\frac{1}{N!}\left[ \frac{8\pi V}{\left( h\beta c\right) ^{3}}\right]
^{N}.$](img9.gif)
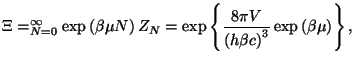
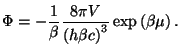
![$\displaystyle Z=\frac{1}{2\pi i}\doint \frac{\Xi \left( \beta ,z,V\right) }{z^{N+1}}dz\sim
\frac{1}{2\pi i}\doint \exp \left[ Nf\left( z\right) \right] dz,$](img13.gif)
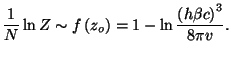
![$\displaystyle \frac{1}{N}\ln Z_{N}=\frac{1}{N}\ln \left\{ \frac{1}{N!}\left[ \frac{8\pi V}{
\left( h\beta c\right) ^{3}}\right] ^{N}\right\}$](img17.gif)
![]() , given by the Hamiltonian
, given by the Hamiltonian
![$\displaystyle \mathcal{H}=\dsum\limits_{i=1}^{N}\left[ \frac{1}{2m}\vec{p}
_{i}^{\,2}+u\left( \vec{r}_{i}\right) \right] .$](img18.gif)
![$\displaystyle \left\langle \left( \Delta N\right) ^{2}\right\rangle =\left\lang...
...z}\left[ z\frac{\partial }{\partial z}\ln \Xi \left( \beta
,z\right) \right] .$](img20.gif)
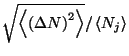 of an
ideal gas of classical monatomic particles.
For a classical ideal gas of monatomic particles, we have
of an
ideal gas of classical monatomic particles.
For a classical ideal gas of monatomic particles, we have
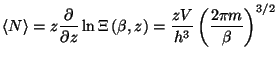
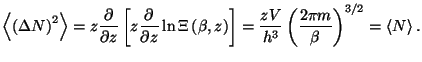
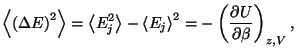
![$\displaystyle \left\langle \left( \Delta E\right) ^{2}\right\rangle =k_{B}T^{2}...
...V}+\frac{\mu }{T}\left(
\frac{\partial U}{\partial \mu }\right) _{T,V}\right]$](img29.gif)
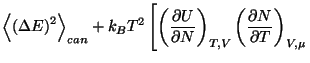
![$\displaystyle +\left. \frac{\mu }{T}\left( \frac{\partial U}{\partial N}\right)
_{T,V}\left( \frac{\partial N}{\partial \mu }\right) _{T,V}\right] ,$](img33.gif)
![$\displaystyle \left[ \left( \frac{\partial U}{\partial N}\right) _{T,V}\left( \...
...l N}\right) _{T,V}\left( \frac{\partial N}{\partial \mu }\right)
_{T,V}\right]$](img35.gif)
![$\displaystyle =\frac{1}{T}\left( \frac{\partial N}{\partial \mu }\right) _{T,V}\left[
\left( \frac{\partial U}{\partial N}\right) _{T,V}\right] ^{2}>0,$](img36.gif)
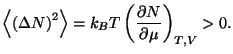
![]() . At a given temperature
. At a given temperature ![]() , a surface with
, a surface with ![]() adsorption centers
has
adsorption centers
has
![]() adsorbed molecules. Suppose that there are no interactions
between molecules. Show that the chemical potential of the adsorbed gas is
given by
adsorbed molecules. Suppose that there are no interactions
between molecules. Show that the chemical potential of the adsorbed gas is
given by
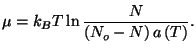
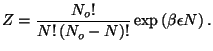
![$\displaystyle \Xi =\dsum\limits_{N}\frac{N_{o}!}{N!\left( N_{o}-N\right) !}\exp...
...N\right) z^{N}=\left[ z\exp \left( \beta \epsilon \right) +1
\right] ^{N_{o}},$](img45.gif)