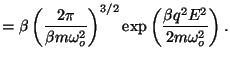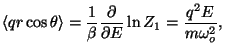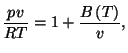Next: About this document ...
Chapter 6- Answers to selected exercises
1. A system of 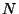 classical ultrarelativistic particles, in a container of
volume
classical ultrarelativistic particles, in a container of
volume 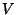 , at temperature
, at temperature 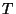 , is given by the Hamiltonian
, is given by the Hamiltonian
where 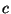 is a positive constant. Obtain an expression for the canonical
partition function. Calculate the entropy per particle as a function of
temperature and specific volume. What is the expression of the specific heat
at constant volume?
All the thermodynamic quantities are easily obtained from the classical
canonical partition function, given by
is a positive constant. Obtain an expression for the canonical
partition function. Calculate the entropy per particle as a function of
temperature and specific volume. What is the expression of the specific heat
at constant volume?
All the thermodynamic quantities are easily obtained from the classical
canonical partition function, given by
2. Consider a set of 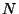 one-dimensional harmonic oscillators, described by
the Hamiltonian
one-dimensional harmonic oscillators, described by
the Hamiltonian
where  is a positive and even integer. Use the canonical formalism to
obtain an expression for the classical specific heat of this system.
Note that the canonical partition function may be written as
is a positive and even integer. Use the canonical formalism to
obtain an expression for the classical specific heat of this system.
Note that the canonical partition function may be written as
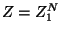 ,
where
,
where
Thus,
3. Consider a classical system of 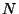 very weakly interacting diatomic
molecules, in a container of volume
very weakly interacting diatomic
molecules, in a container of volume 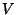 , at a given temperature
, at a given temperature 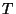 . The
Hamiltonian of a single molecule is given by
. The
Hamiltonian of a single molecule is given by
where 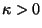 is an elastic constant. Obtain an expression for the
Helmholtz free energy of this system. Calculate the specific heat at
constant volume. Calculate the mean molecular diameter,
is an elastic constant. Obtain an expression for the
Helmholtz free energy of this system. Calculate the specific heat at
constant volume. Calculate the mean molecular diameter,
Now consider another Hamiltonian, of the form 
where  and
and 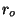 are positive constants, and
are positive constants, and
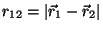 . What are the changes in your previous
answers?
Taking into account the thermodynamic limit (
. What are the changes in your previous
answers?
Taking into account the thermodynamic limit (
 ), the
first Hamiltonian is associated with the partition function
), the
first Hamiltonian is associated with the partition function
from which we obtain the Helmholtz free energy (and the value of  ). It
interesting to check the constant value of the molecular specific heat,
). It
interesting to check the constant value of the molecular specific heat,
 .
The second Hamiltonian represents a more complicated model of a diatomic
molecule. The partition function is given by
.
The second Hamiltonian represents a more complicated model of a diatomic
molecule. The partition function is given by
where
Now it is interesting to obtain the specific heat as a function of
temperature.
4. Neglecting the vibrational motion, a diatomic molecule may be treated as
a three-dimensional rigid rotator. The Hamiltonian
 of the
molecule is written as a sum of a translational,
of the
molecule is written as a sum of a translational,
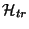 , plus a
rotational,
, plus a
rotational,
 , term (that is,
, term (that is,
 ). Consider a system of
). Consider a system of 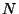 very weakly interacting
molecules of this kind, in a container of volume
very weakly interacting
molecules of this kind, in a container of volume 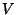 , at a given temperature
, at a given temperature
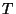 .
(a) Obtain an expression for
.
(a) Obtain an expression for
 in spherical coordinates.
Show that there is a factorization of the canonical partition function of
this system. Obtain an expression for the specific heat at constant volume.
(b) Now suppose that each molecule has a permanent electric dipole moment
in spherical coordinates.
Show that there is a factorization of the canonical partition function of
this system. Obtain an expression for the specific heat at constant volume.
(b) Now suppose that each molecule has a permanent electric dipole moment 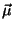 and that the system is in the presence of an external electric
field
and that the system is in the presence of an external electric
field 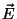 (with the dipole
(with the dipole 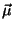 along the axis of the rotor).
What is the form of the new rotational part of the Hamiltonian? Obtain an
expression for the polarization of the molecule as a function of field and
temperature. Calculate the electric susceptibility of this system.
The Lagrangian of a free rotator (two atoms of mass
along the axis of the rotor).
What is the form of the new rotational part of the Hamiltonian? Obtain an
expression for the polarization of the molecule as a function of field and
temperature. Calculate the electric susceptibility of this system.
The Lagrangian of a free rotator (two atoms of mass 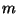 and a fixed
interatomic distance
and a fixed
interatomic distance 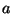 ) is given by
) is given by
from which we have the Hamiltonian
Therefore,
In the presence on an electric field (taken along the 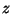 direction), and
with the magnetic moment along the axis of the rotator, we have
direction), and
with the magnetic moment along the axis of the rotator, we have
The associated partition function is given by
Thus, we have
where
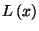 is known as the Langevin function.
is known as the Langevin function.
5. Consider a classical gas of 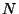 weakly interacting molecules, at
temperature
weakly interacting molecules, at
temperature 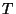 , in an applied electric field
, in an applied electric field 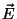 . Since there is no
permanent electric dipole moment, the polarization of this system comes from
the induction by the field. We then suppose that the Hamiltonian of each
molecule will be given by the sum of a standard translational term plus an
``internal term.'' This internal term involves an isotropic elastic energy,
which tends to preserve the shape of the molecule, and a term of interaction
with the electric field. The configurational part of the internal
Hamiltonian is be given by
. Since there is no
permanent electric dipole moment, the polarization of this system comes from
the induction by the field. We then suppose that the Hamiltonian of each
molecule will be given by the sum of a standard translational term plus an
``internal term.'' This internal term involves an isotropic elastic energy,
which tends to preserve the shape of the molecule, and a term of interaction
with the electric field. The configurational part of the internal
Hamiltonian is be given by
Obtain the polarization per molecule as a function of field and temperature.
Obtain the electric susceptibility. Compare with the results of the last
problem. Make some comments about the main differences between these
results. Do you know any physical examples corresponding to these models?
First, we calculate the configurational partition function
The polarization is given by
so the dielectric susceptibility is just a constant (in sharp contrast to
the previous result for permanent electric dipoles!)
6. The equation of state of gaseous nitrogen at low densities may be written
as
where 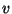 is a molar volume,
is a molar volume, 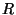 is the universal gas constant, and
is the universal gas constant, and
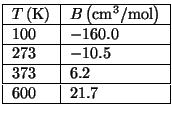
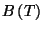 is a function of temperature only. In the following table we give
some experimental data for the second virial coefficient,
is a function of temperature only. In the following table we give
some experimental data for the second virial coefficient,
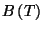 , as a function of temperature.
, as a function of temperature.
Suppose that the intermolecular potential of gaseous nitrogen is given by
Use the experimental data of this table to determine the best values of the
parameters 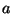 ,
,  , and
, and  .
According to Section 6.4 (although nitrogen is a gas of diatomic molecules),
the virial coefficient is given by
.
According to Section 6.4 (although nitrogen is a gas of diatomic molecules),
the virial coefficient is given by
Now it is straightforward to fit the parameters 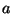 ,
,  and
and  .
.



Next: About this document ...
Jairo da Silva
2001-03-12
![$\displaystyle Z=\frac{1}{h^{3N}N!}V^{N}\left[ \dint d^{3}p\exp \left( -\beta c\...
...rac{1}{h^{3N}N!}\left[
\frac{8\pi V}{\left( \beta c\right) ^{3}}\right] ^{N}.$](img6.gif)
![]() one-dimensional harmonic oscillators, described by
the Hamiltonian
one-dimensional harmonic oscillators, described by
the Hamiltonian
![$\displaystyle \mathcal{H}=\dsum\limits_{i=1}^{N}\left[ \frac{1}{2m}\vec{p}_{i}^{\,2}+\frac{
1}{2}m\omega ^{2}x_{i}^{n}\right] ,$](img7.gif)
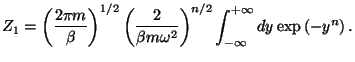
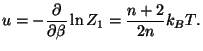
![]() very weakly interacting diatomic
molecules, in a container of volume
very weakly interacting diatomic
molecules, in a container of volume ![]() , at a given temperature
, at a given temperature ![]() . The
Hamiltonian of a single molecule is given by
. The
Hamiltonian of a single molecule is given by

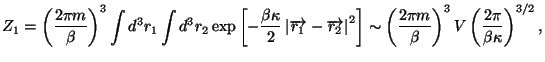
![$\displaystyle Z_{1}=\left( \frac{2\pi m}{\beta }\right) ^{3}\int d^{3}r_{1}\int...
...o}\right) \right\vert \right] \sim
\left( \frac{2\pi m}{\beta }\right) ^{3}VI,$](img23.gif)
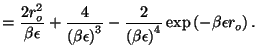
![]() of the
molecule is written as a sum of a translational,
of the
molecule is written as a sum of a translational,
![]() , plus a
rotational,
, plus a
rotational,
![]() , term (that is,
, term (that is,
![]() ). Consider a system of
). Consider a system of ![]() very weakly interacting
molecules of this kind, in a container of volume
very weakly interacting
molecules of this kind, in a container of volume ![]() , at a given temperature
, at a given temperature
![]() .
(a) Obtain an expression for
.
(a) Obtain an expression for
![]() in spherical coordinates.
Show that there is a factorization of the canonical partition function of
this system. Obtain an expression for the specific heat at constant volume.
(b) Now suppose that each molecule has a permanent electric dipole moment
in spherical coordinates.
Show that there is a factorization of the canonical partition function of
this system. Obtain an expression for the specific heat at constant volume.
(b) Now suppose that each molecule has a permanent electric dipole moment ![]() and that the system is in the presence of an external electric
field
and that the system is in the presence of an external electric
field ![]() (with the dipole
(with the dipole ![]() along the axis of the rotor).
What is the form of the new rotational part of the Hamiltonian? Obtain an
expression for the polarization of the molecule as a function of field and
temperature. Calculate the electric susceptibility of this system.
The Lagrangian of a free rotator (two atoms of mass
along the axis of the rotor).
What is the form of the new rotational part of the Hamiltonian? Obtain an
expression for the polarization of the molecule as a function of field and
temperature. Calculate the electric susceptibility of this system.
The Lagrangian of a free rotator (two atoms of mass ![]() and a fixed
interatomic distance
and a fixed
interatomic distance ![]() ) is given by
) is given by
![$\displaystyle L_{rot}=\frac{ma^{2}}{4}\overset{}{\left[ \left( \frac{d\theta }{dt}\right)
^{2}+\left( \frac{d\varphi }{dt}\right) ^{2}\sin ^{2}\theta \right] },$](img34.gif)

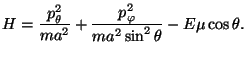
![$\displaystyle Z_{1}=\dint\limits_{0}^{\pi }d\theta \dint\limits_{0}^{2\pi }d\va...
...ta p_{\varphi }^{2}}{ma^{2}\sin ^{2}\theta }+\beta E\mu \cos \theta
.\right] =$](img39.gif)
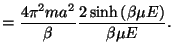
![$\displaystyle \left\langle \mu \cos \theta \right\rangle =\mu \left[ \coth \lef...
...a
\mu E\right) -\frac{1}{\beta \mu E}\right] =\mu L\left( \beta \mu E\right) ,$](img41.gif)
![]() weakly interacting molecules, at
temperature
weakly interacting molecules, at
temperature ![]() , in an applied electric field
, in an applied electric field ![]() . Since there is no
permanent electric dipole moment, the polarization of this system comes from
the induction by the field. We then suppose that the Hamiltonian of each
molecule will be given by the sum of a standard translational term plus an
``internal term.'' This internal term involves an isotropic elastic energy,
which tends to preserve the shape of the molecule, and a term of interaction
with the electric field. The configurational part of the internal
Hamiltonian is be given by
. Since there is no
permanent electric dipole moment, the polarization of this system comes from
the induction by the field. We then suppose that the Hamiltonian of each
molecule will be given by the sum of a standard translational term plus an
``internal term.'' This internal term involves an isotropic elastic energy,
which tends to preserve the shape of the molecule, and a term of interaction
with the electric field. The configurational part of the internal
Hamiltonian is be given by
![$\displaystyle Z_{1}=\dint\limits_{0}^{\infty }r^{2}dr\dint\limits_{0}^{\pi }\si...
...p \left[ -\frac{\beta m\omega
_{o}^{2}}{2}r^{2}+\beta qEr\cos \theta \right] =$](img44.gif)