


Next: About this document ...
Chapter 5- Answers to selected exercises
1. The energy of a system of 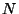 localized magnetic ions, at temperature
localized magnetic ions, at temperature 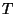 , in the presence of a field
, in the presence of a field 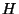 , may be written as
, may be written as
where the parameters  ,
, 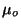 , and
, and 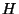 are positive, and
are positive, and 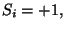
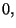 or
or 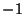 , for all sites
, for all sites  . Obtain expressions for the internal energy,
the entropy, and the magnetization per site. In zero field (
. Obtain expressions for the internal energy,
the entropy, and the magnetization per site. In zero field (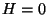 ), sketch
graphs of the internal energy, the entropy, and the specific heat versus
temperature. Indicate the behavior of these quantities in the limits
), sketch
graphs of the internal energy, the entropy, and the specific heat versus
temperature. Indicate the behavior of these quantities in the limits
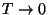 and
and
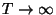 . Calculate the expected value of
the ``quadrupole moment,''
. Calculate the expected value of
the ``quadrupole moment,''
as a function of field and temperature.
The canonical partition function is given by
The internal energy per ion comes from
The magnetization per spin is given by
and the ``quadrupolar moment'' by
In zero field, we have
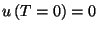 ,
,
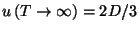 ,
,
 , and
, and
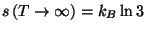 .
.
2. Consider a one-dimensional magnetic system of 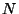 localized spins, at
temperature
localized spins, at
temperature 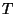 , associated with the energy
, associated with the energy
where the parameters 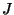 ,
, 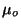 , and
, and 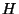 are positive, and
are positive, and
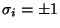 for all sites
for all sites  . Assume that
. Assume that 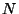 is an even number, and note
that the first sum is over odd integers.
(a) Obtain an expression for the canonical partition function and calculate
the internal energy per spin,
is an even number, and note
that the first sum is over odd integers.
(a) Obtain an expression for the canonical partition function and calculate
the internal energy per spin,
 . Sketch a graph of
. Sketch a graph of
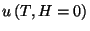 versus temperature
versus temperature 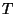 . Obtain an expression for the
entropy per spin,
. Obtain an expression for the
entropy per spin,
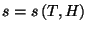 . Sketch a graph of
. Sketch a graph of
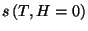 versus
versus 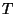 .
(b) Obtain expressions for the magnetization per particle,
.
(b) Obtain expressions for the magnetization per particle, 
and for the magnetic susceptibility,
Sketch a graph of
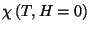 versus temperature.
The canonical partition function is given by
versus temperature.
The canonical partition function is given by
The magnetization per particle is given by
whose derivative with respect to 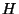 yields the susceptibility.
yields the susceptibility.
3. Consider a system of 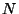 classical and noninteracting particles in
contact with a thermal reservoir at temperature
classical and noninteracting particles in
contact with a thermal reservoir at temperature 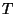 . Each particle may have
energies 0,
. Each particle may have
energies 0,
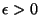 , or
, or 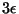 . Obtain an expression for the
canonical partition function, and calculate the internal energy per
particle,
. Obtain an expression for the
canonical partition function, and calculate the internal energy per
particle,
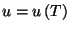 . Sketch a graph of
. Sketch a graph of 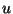 versus
versus 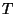 (indicate
the values of
(indicate
the values of 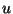 in the limits
in the limits
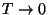 and
and
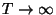 ). Calculate the entropy per particle,
). Calculate the entropy per particle,
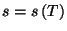 , and sketch a
graph of
, and sketch a
graph of 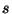 versus
versus 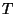 . Sketch a graph of the specific heat versus
temperature.
The canonical partition function is given by
. Sketch a graph of the specific heat versus
temperature.
The canonical partition function is given by
For
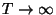 , we have
, we have
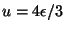 and
and
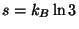 .
.
4. A system of 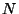 localized and independent quantum oscillators is in
contact with a thermal reservoir at temperature
localized and independent quantum oscillators is in
contact with a thermal reservoir at temperature 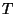 . The energy levels of
each oscillator are given by
. The energy levels of
each oscillator are given by
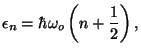 with with 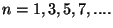 |
|
Note that 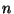 is an odd integer.
(a) Obtain an expression for the internal energy
is an odd integer.
(a) Obtain an expression for the internal energy 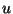 per oscillator as a
function of temperature
per oscillator as a
function of temperature 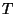 . What is the form of
. What is the form of 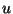 in the classical limit (
in the classical limit (
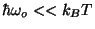 )?
(b) Obtain an expression for the entropy per oscillator as a function of
temperature. Sketch a graph of entropy
)?
(b) Obtain an expression for the entropy per oscillator as a function of
temperature. Sketch a graph of entropy  versus temperature. What is
the expression of the entropy in the classical limit?
(c) What is the expression of the specific heat in the classical limit?
The answers come from the expression
versus temperature. What is
the expression of the entropy in the classical limit?
(c) What is the expression of the specific heat in the classical limit?
The answers come from the expression
The internal energy is given by
Note that
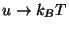 in the classical limit (the specific heat is
just
in the classical limit (the specific heat is
just 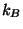 ).
).
5. Consider a system of 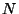 noninteracting classical particles. The
single-particle states have energies
noninteracting classical particles. The
single-particle states have energies
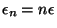 , and are
, and are 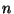 times degenerate (
times degenerate (
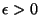 ;
;
 ). Calculate the canonical
partition function and the entropy of this system. Obtain expressions for
the internal energy and the entropy as a function of temperature. What are
the expressions for the entropy and the specific heat in the limit of high
temperatures?
The thermodynamic functions come from canonical partition function, given by
). Calculate the canonical
partition function and the entropy of this system. Obtain expressions for
the internal energy and the entropy as a function of temperature. What are
the expressions for the entropy and the specific heat in the limit of high
temperatures?
The thermodynamic functions come from canonical partition function, given by
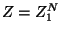 , where
, where
6. A set of 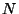 classical oscillators in one dimension is given by the
Hamiltonian
classical oscillators in one dimension is given by the
Hamiltonian
Using the formalism of the canonical ensemble in classical phase space,
obtain expressions for the partition function, the energy per oscillator,
the entropy per oscillator, and the specific heat. Compare with the results
from the classical limit of the quantum oscillator. Calculate an expression
for the quadratic deviation of the energy as a function of temperature.
The thermodynamic functions come from canonical partition function, given by
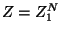 , where
, where
 7. Consider again the preceding problem. The canonical
partition function can be written as an integral form,
7. Consider again the preceding problem. The canonical
partition function can be written as an integral form,
where
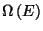 is the number of accessible microscopic
states of the system with energy
is the number of accessible microscopic
states of the system with energy 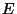 . Note that, in the expressions for
. Note that, in the expressions for
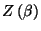 and
and
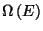 , we are omitting the
dependence on the number
, we are omitting the
dependence on the number 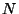 of oscillators. Using the expression for
of oscillators. Using the expression for
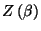 obtained in the last exercise, perform a
reverse Laplace transformation to obtain an asymptotic form (in the
thermodynamic limit) for
obtained in the last exercise, perform a
reverse Laplace transformation to obtain an asymptotic form (in the
thermodynamic limit) for
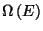 . Compare with the
expression calculated in the framework of the microcanonical ensemble.
First, we use an integral representation of the
. Compare with the
expression calculated in the framework of the microcanonical ensemble.
First, we use an integral representation of the 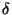 -function (see
Appendix) to see that
-function (see
Appendix) to see that
Using the result of the previous exercise, we have
which can be written in the form of a saddle-point integration (see
Appendix),
where 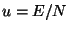 . Using the asymptotic integration techniques of the Appendix,
we locate the saddle point at
. Using the asymptotic integration techniques of the Appendix,
we locate the saddle point at
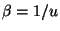 and write the asymptotic form
(for
and write the asymptotic form
(for
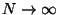 ),
),
Therefore, we have the entropy per oscillator,
which should be compared with the well-known result for the classical
one-dimensional harmonic oscillator in the microcanonical ensemble.
8. A system of 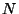 one-dimensional localized oscillators, at a given
temperature
one-dimensional localized oscillators, at a given
temperature 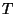 , is associated with the Hamiltonian
, is associated with the Hamiltonian
where
with
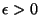 .
(a) Obtain the canonical partition function of this classical system.
Calculate the internal energy per oscillator,
.
(a) Obtain the canonical partition function of this classical system.
Calculate the internal energy per oscillator,
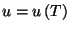 . What is
the form of
. What is
the form of
 in the limits
in the limits
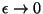 and
and
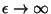 ?
(b) Consider now the quantum analog of this model in the limit
?
(b) Consider now the quantum analog of this model in the limit
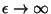 . Obtain an expression for the canonical partition
function. What is the internal energy per oscillator of this quantum analog?
The classical partition function is given by
. Obtain an expression for the canonical partition
function. What is the internal energy per oscillator of this quantum analog?
The classical partition function is given by
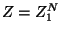 , where
, where
Note that we have
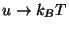 for both limits,
for both limits,
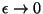 and
and
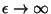 .
In order to write the quantum partition function, in the
.
In order to write the quantum partition function, in the
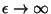 limit, we should consider odd values of
limit, we should consider odd values of 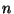 only (note
that even values of
only (note
that even values of 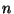 are associated with wave functions that do not
vanish at the origin).
are associated with wave functions that do not
vanish at the origin).



Next: About this document ...
Jairo da Silva
2001-03-12

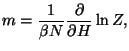
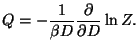
![]() localized spins, at
temperature
localized spins, at
temperature ![]() , associated with the energy
, associated with the energy

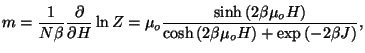
![]() classical and noninteracting particles in
contact with a thermal reservoir at temperature
classical and noninteracting particles in
contact with a thermal reservoir at temperature ![]() . Each particle may have
energies 0,
. Each particle may have
energies 0,
![]() , or
, or ![]() . Obtain an expression for the
canonical partition function, and calculate the internal energy per
particle,
. Obtain an expression for the
canonical partition function, and calculate the internal energy per
particle,
![]() . Sketch a graph of
. Sketch a graph of ![]() versus
versus ![]() (indicate
the values of
(indicate
the values of ![]() in the limits
in the limits
![]() and
and
![]() ). Calculate the entropy per particle,
). Calculate the entropy per particle,
![]() , and sketch a
graph of
, and sketch a
graph of ![]() versus
versus ![]() . Sketch a graph of the specific heat versus
temperature.
The canonical partition function is given by
. Sketch a graph of the specific heat versus
temperature.
The canonical partition function is given by
![]() localized and independent quantum oscillators is in
contact with a thermal reservoir at temperature
localized and independent quantum oscillators is in
contact with a thermal reservoir at temperature ![]() . The energy levels of
each oscillator are given by
. The energy levels of
each oscillator are given by
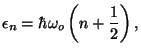 with
with 
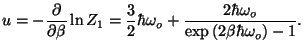
![]() noninteracting classical particles. The
single-particle states have energies
noninteracting classical particles. The
single-particle states have energies
![]() , and are
, and are ![]() times degenerate (
times degenerate (
![]() ;
;
![]() ). Calculate the canonical
partition function and the entropy of this system. Obtain expressions for
the internal energy and the entropy as a function of temperature. What are
the expressions for the entropy and the specific heat in the limit of high
temperatures?
The thermodynamic functions come from canonical partition function, given by
). Calculate the canonical
partition function and the entropy of this system. Obtain expressions for
the internal energy and the entropy as a function of temperature. What are
the expressions for the entropy and the specific heat in the limit of high
temperatures?
The thermodynamic functions come from canonical partition function, given by
![]() , where
, where
![$\displaystyle Z_{1}=\dsum\limits_{n=1,2,3,...}n\exp \left( -\beta n\epsilon \ri...
... \epsilon \right) }{\left[ \exp \left( \beta \epsilon
\right) -1\right] ^{2}}.$](img56.gif)
![]() classical oscillators in one dimension is given by the
Hamiltonian
classical oscillators in one dimension is given by the
Hamiltonian
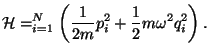
![$\displaystyle Z_{1}=\dint\limits_{-\infty }^{+\infty }\dint\limits_{-\infty }^{...
...}p^{2}-\frac{\beta m\omega ^{2}}{2}q^{2}
\right] =\frac{2\pi }{\beta \omega }.$](img58.gif)
![]() 7. Consider again the preceding problem. The canonical
partition function can be written as an integral form,
7. Consider again the preceding problem. The canonical
partition function can be written as an integral form,
![$\displaystyle \frac{1}{2\pi }\dint\limits_{-i\infty }^{+i\infty }Z\left( \beta ...
...\left( E^{\prime }-E\right) \right] d\beta =\Omega \left(
E^{\prime }\right) .$](img65.gif)
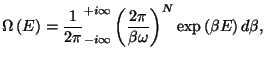
![$\displaystyle \Omega \left( E\right) =\frac{1}{2\pi }\dint\limits_{-i\infty }^{...
...eft( \frac{2\pi }{\omega }\right) -\ln \beta
+u\beta \right] \right\} d\beta ,$](img67.gif)
![$\displaystyle \Omega \left( E\right) \sim \left( 2\pi u^{2}\right) ^{-1/2}\exp ...
...\{ N
\left[ \ln \left( \frac{2\pi }{\omega }\right) +\ln u+1\right] \right\} .$](img71.gif)
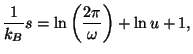
![]() one-dimensional localized oscillators, at a given
temperature
one-dimensional localized oscillators, at a given
temperature ![]() , is associated with the Hamiltonian
, is associated with the Hamiltonian
![$\displaystyle \mathcal{H}=\dsum\limits_{i=1}^{N}\left[ \frac{1}{2m}p_{i}^{2}+V\left(
q_{i}\right) \right] ,$](img73.gif)
