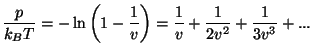Next: About this document ...
Chapter 4- Answers to selected exercises
1. Consider a model of 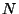 localized magnetic ions, given by the spin
Hamiltonian
localized magnetic ions, given by the spin
Hamiltonian
where the spin variable  may assume the values
may assume the values 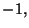
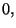 or
or 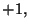 for all
for all 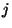 (see exercise 8 of Chapter 2). Given the total energy
(see exercise 8 of Chapter 2). Given the total energy 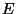 , use the expression for the number of accessible microstates,
, use the expression for the number of accessible microstates,
 to obtain the entropy per particle,
to obtain the entropy per particle,
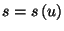 , where
, where 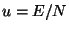 . Obtain an expression for the specific heat
. Obtain an expression for the specific heat 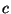 in terms of
the temperature
in terms of
the temperature  . Sketch a graph of
. Sketch a graph of 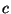 versus
versus  . Check the existence
of a broad maximum associated with the Schottky effect. Write an expression
for the entropy as a function of temperature. What are the limiting values
of the entropy for
. Check the existence
of a broad maximum associated with the Schottky effect. Write an expression
for the entropy as a function of temperature. What are the limiting values
of the entropy for
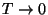 and
and
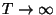 ?
The entropy per particle is given by
?
The entropy per particle is given by
where 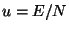 . Thus, we have the equation of state
. Thus, we have the equation of state
from which we have
where
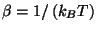 . The specific heat is given by the
derivative of
. The specific heat is given by the
derivative of 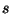 with respect to
with respect to  .
For
.
For
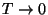 ,
,
 ; for
; for
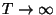 ,
,
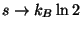 .
.
2. In the solid of Einstein, we may introduce a volume coordinate if we make
the phenomenological assumption that the fundamental frequency 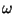 as
a function of
as
a function of  is given by =
is given by =
where
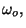
 , and
, and 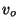 are positive constants. Obtain
expressions for the expansion coefficient and the isothermal compressibility
of this model system.
As
are positive constants. Obtain
expressions for the expansion coefficient and the isothermal compressibility
of this model system.
As
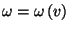 , the entropy of Einstein's solid can be
written as a function of energy and volume,
, the entropy of Einstein's solid can be
written as a function of energy and volume,
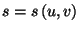 . From
the equations of state, it is straightforward to obtain the expansion
coefficient and the compressibility.
. From
the equations of state, it is straightforward to obtain the expansion
coefficient and the compressibility.
3. Consider the semiclassical model of 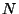 particles with two energy levels (
0 and
particles with two energy levels (
0 and
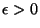 ). As in the previous exercise, suppose that the volume
of the gas may be introduced by the assumption that the energy of the
excited level depends on
). As in the previous exercise, suppose that the volume
of the gas may be introduced by the assumption that the energy of the
excited level depends on  ,
,
where 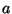 and
and 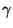 are positive constants. Obtain an equation of state
for the pressure,
are positive constants. Obtain an equation of state
for the pressure,
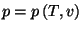 , and an expression for the
isothermal compressibility (note that the constant
, and an expression for the
isothermal compressibility (note that the constant 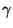 plays the role
of the Grüneisen parameter of the solid).
Again, as
plays the role
of the Grüneisen parameter of the solid).
Again, as
 , we can write
, we can write
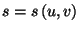 . From the equations of state, it is easy to write the
isothermal compressibility.
. From the equations of state, it is easy to write the
isothermal compressibility.
4. The total number of the accessible microscopic states of the Boltzmann
gas, with energy 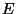 and number of particles
and number of particles 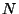 , may be written as
, may be written as
with the restrictions
 and and 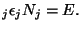 |
|
Except for an additive constant, show that the entropy per particle is given
by
where
 is the set of occupation numbers at
equilibrium. Using the continuum limit of the Boltzmann gas, show that the
entropy depends on temperature according to a term of the form
is the set of occupation numbers at
equilibrium. Using the continuum limit of the Boltzmann gas, show that the
entropy depends on temperature according to a term of the form
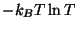 .
.
5. Consider a lattice gas of 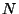 particles distributed among
particles distributed among  cells (with
cells (with
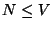 ). Suppose that each cell may be either empty or occupied by a
single particle. The number of microscopic states of this system will be
given by
). Suppose that each cell may be either empty or occupied by a
single particle. The number of microscopic states of this system will be
given by
Obtain an expression for the entropy per particle,
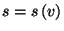 ,
where
,
where  . From this fundamental equation, obtain an expression for the
equation of state
. From this fundamental equation, obtain an expression for the
equation of state 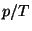 . Write an expansion of
. Write an expansion of 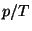 in terms of the density
in terms of the density
 . Show that the first term of this expansion gives the Boyle law
of the ideal gases. Sketch a graph of
. Show that the first term of this expansion gives the Boyle law
of the ideal gases. Sketch a graph of 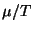 , where
, where  is the chemical
potential, in terms of the density
is the chemical
potential, in terms of the density 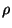 . What is the behavior of the
chemical potential in the limits
. What is the behavior of the
chemical potential in the limits
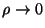 and
and
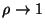 ?
The entropy particle is given by
?
The entropy particle is given by
Thus, we have the equation of state
Note that Bolyles's law is already given by the first term is this expansion.
To find 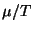 , we write
, we write
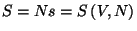 , and take the
derivative with respect to
, and take the
derivative with respect to 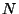 .
.



Next: About this document ...
Jairo da Silva
2001-03-12
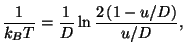

![]() as
a function of
as
a function of ![]() is given by =
is given by =
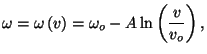
![]() particles with two energy levels (
0 and
particles with two energy levels (
0 and
![]() ). As in the previous exercise, suppose that the volume
of the gas may be introduced by the assumption that the energy of the
excited level depends on
). As in the previous exercise, suppose that the volume
of the gas may be introduced by the assumption that the energy of the
excited level depends on ![]() ,
,
![]() and number of particles
and number of particles ![]() , may be written as
, may be written as
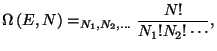
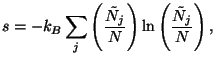
![]() particles distributed among
particles distributed among ![]() cells (with
cells (with
![]() ). Suppose that each cell may be either empty or occupied by a
single particle. The number of microscopic states of this system will be
given by
). Suppose that each cell may be either empty or occupied by a
single particle. The number of microscopic states of this system will be
given by