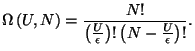Next: About this document ...
Chapter 2 - Answers to selected exercises
1. Neglect the complexities of classical phase space, and consider a system
of  distinguishable and noninteracting particles, which may be found in
two states of energy, with
distinguishable and noninteracting particles, which may be found in
two states of energy, with
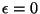 and
and
 , respectively.
Given the total energy
, respectively.
Given the total energy  of this system, obtain an expression for the
associated number of microscopic states.
of this system, obtain an expression for the
associated number of microscopic states.
2. Calculate the number of accessible microscopic states of a system of two
localized and independent quantum oscillators, with fundamental frequencies
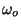 and
and
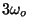 , respectively, and total energy
, respectively, and total energy
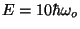 .
.
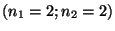 ;
;
 ;
;
 .
.
3. Consider a classical one-dimensional system of two noninteracting
particles of the same mass  The motion of the particles is restricted to
a region of the
The motion of the particles is restricted to
a region of the 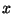 axis between
axis between 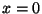 and
and 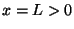 . Let
. Let 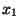 and
and 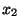 be the position coordinates of the particles, and
be the position coordinates of the particles, and 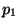 and
and 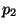 be the
canonically conjugated momenta. The total energy of the system is between
be the
canonically conjugated momenta. The total energy of the system is between 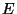 and
and
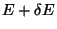 . Draw the projection of phase space in a plane defined by
position coordinates. Indicate the region of this plane that is accessible
to the system. Draw similar graphs in the plane defined by the momentum
coordinates.
. Draw the projection of phase space in a plane defined by
position coordinates. Indicate the region of this plane that is accessible
to the system. Draw similar graphs in the plane defined by the momentum
coordinates.
4. The position of a one-dimensional harmonic oscillator is given by
where 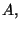
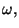 and
and 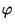 are positive constants. Obtain
are positive constants. Obtain
 , that is, the probability of finding the oscillator with
position between
, that is, the probability of finding the oscillator with
position between 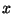 and
and 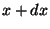 . Note that it is enough to calculate
. Note that it is enough to calculate 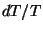 ,
where
,
where 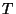 is a period of oscillation, and
is a period of oscillation, and 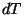 is an interval of time,
within a period, in which the amplitude remains between
is an interval of time,
within a period, in which the amplitude remains between 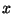 and
and 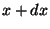 . Draw
a graph of
. Draw
a graph of 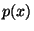 versus
versus 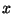 .
.
5. Now consider the classical phase space of an ensemble of identical
one-dimensional oscillators with energy between 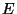 and
and
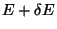 . Given
the energy
. Given
the energy 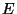 , we have an ellipse in phase space. So, the accessible region
in phase space is a thin elliptical shell bounded by the ellipses associated
with energies
, we have an ellipse in phase space. So, the accessible region
in phase space is a thin elliptical shell bounded by the ellipses associated
with energies 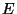 and
and
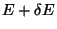 , respectively. Obtain an expression for
the small area
, respectively. Obtain an expression for
the small area 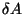 of this elliptical shell between
of this elliptical shell between 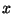 and
and 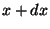 .
Show that the probability
.
Show that the probability 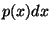 may also be given by
may also be given by
 , where
, where 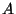 is the total area of the elliptical shell. This is one of the few
examples where we can check the validity of the ergodic hypothesis and the
postulate of equal a priori probabilities.
6. Consider a classical system of
is the total area of the elliptical shell. This is one of the few
examples where we can check the validity of the ergodic hypothesis and the
postulate of equal a priori probabilities.
6. Consider a classical system of 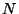 localized and weakly interacting
one-dimensional harmonic oscillators, whose Hamiltonian is written as
localized and weakly interacting
one-dimensional harmonic oscillators, whose Hamiltonian is written as
where 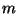 is the mass and
is the mass and  is an elastic constant. Obtain the accessible
volume of phase space for
is an elastic constant. Obtain the accessible
volume of phase space for
 , with
, with
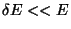 . This classical model for the elastic vibrations of a solid leads to a
constant specific heat with temperature (law of Dulong and Petit). The solid
of Einstein is a quantum version of this model. The specific heat of
Einstein's model decreases with temperature, in qualitative agreement with
experimental data.
. This classical model for the elastic vibrations of a solid leads to a
constant specific heat with temperature (law of Dulong and Petit). The solid
of Einstein is a quantum version of this model. The specific heat of
Einstein's model decreases with temperature, in qualitative agreement with
experimental data.
where
 is the volume of a hyperspherical shell (see Appendix)
of radius
is the volume of a hyperspherical shell (see Appendix)
of radius 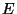 and thickness
and thickness 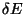 .
.
7. The spin Hamiltonian of a system of 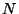 localized magnetic ions is given
by
localized magnetic ions is given
by
where 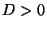 and the spin variable
and the spin variable 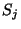 may assume the values
may assume the values 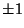 or
or 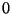 , for all
, for all
 . This spin Hamiltonian describes the effects of the
electrostatic environment on spin-
. This spin Hamiltonian describes the effects of the
electrostatic environment on spin-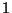 ions. An ion in states
ions. An ion in states 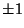 has
energy
has
energy 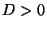 , and an ion in state 0 has zero energy. Show that the number
of accessible microscopic states of this system with total energy
, and an ion in state 0 has zero energy. Show that the number
of accessible microscopic states of this system with total energy  can be
written as
can be
written as
for 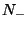 ranging from 0 to
ranging from 0 to 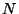 , with
, with 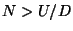 and
and  . Thus, we
have
. Thus, we
have
Using Stirling's asymptotic series, show that
for
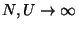 , with
, with 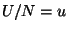 fixed. This last expression is
the entropy per particle in units of Boltzmann's constant,
fixed. This last expression is
the entropy per particle in units of Boltzmann's constant,  .
.
8. In a simplified model of a gas of particles, the system is divided into 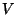 cells of unit volume. Find the number of ways to distribute
cells of unit volume. Find the number of ways to distribute 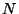 distinguishable particles (with
distinguishable particles (with
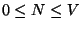 ) within
) within 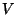 cells, such that
each cell may be either empty or filled up by only one particle. How would
your answer be modified for indistinguishable particles?
cells, such that
each cell may be either empty or filled up by only one particle. How would
your answer be modified for indistinguishable particles?
and
9. The atoms of a crystalline solid may occupy either a position of
equilibrium, with zero energy, or a displaced position, with energy
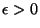 . To each equilibrium position, there corresponds a unique
displaced position. Given the number
. To each equilibrium position, there corresponds a unique
displaced position. Given the number 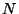 of atoms, and the total energy
of atoms, and the total energy  ,
calculate the number of accessible microscopic states of this system.
,
calculate the number of accessible microscopic states of this system.



Next: About this document ...
Jairo da Silva
2001-03-12
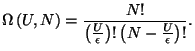
![]() and
and
![]() , respectively, and total energy
, respectively, and total energy
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
![]() The motion of the particles is restricted to
a region of the
The motion of the particles is restricted to
a region of the ![]() axis between
axis between ![]() and
and ![]() . Let
. Let ![]() and
and ![]() be the position coordinates of the particles, and
be the position coordinates of the particles, and ![]() and
and ![]() be the
canonically conjugated momenta. The total energy of the system is between
be the
canonically conjugated momenta. The total energy of the system is between ![]() and
and
![]() . Draw the projection of phase space in a plane defined by
position coordinates. Indicate the region of this plane that is accessible
to the system. Draw similar graphs in the plane defined by the momentum
coordinates.
. Draw the projection of phase space in a plane defined by
position coordinates. Indicate the region of this plane that is accessible
to the system. Draw similar graphs in the plane defined by the momentum
coordinates.
![$\displaystyle p\left( x\right) =\frac{1}{2\pi A}\left[ 1-\left( \frac{x}{A}\right) ^{2}
\right] ^{-1/2}.$](img32.gif)
![]() and
and
![]() . Given
the energy
. Given
the energy ![]() , we have an ellipse in phase space. So, the accessible region
in phase space is a thin elliptical shell bounded by the ellipses associated
with energies
, we have an ellipse in phase space. So, the accessible region
in phase space is a thin elliptical shell bounded by the ellipses associated
with energies ![]() and
and
![]() , respectively. Obtain an expression for
the small area
, respectively. Obtain an expression for
the small area ![]() of this elliptical shell between
of this elliptical shell between ![]() and
and ![]() .
Show that the probability
.
Show that the probability ![]() may also be given by
may also be given by
![]() , where
, where ![]() is the total area of the elliptical shell. This is one of the few
examples where we can check the validity of the ergodic hypothesis and the
postulate of equal a priori probabilities.
6. Consider a classical system of
is the total area of the elliptical shell. This is one of the few
examples where we can check the validity of the ergodic hypothesis and the
postulate of equal a priori probabilities.
6. Consider a classical system of ![]() localized and weakly interacting
one-dimensional harmonic oscillators, whose Hamiltonian is written as
localized and weakly interacting
one-dimensional harmonic oscillators, whose Hamiltonian is written as

![]() localized magnetic ions is given
by
localized magnetic ions is given
by
![$\displaystyle \Omega \left( U,N\right) =\frac{N!}{\left( N-\frac{U}{D}\right) !...
...sum\limits_{N_{-}}\left[ \left( \frac{U}{D}-N_{-}\right) !N_{-}!\right]
^{-1},$](img52.gif)
![$\displaystyle \Omega \left( U,N\right) =N!2^{U/D}\left[ \left( N-\frac{U}{D}\right)
!\left( \frac{U}{D}\right) !\right] ^{-1}.$](img56.gif)
![]() cells of unit volume. Find the number of ways to distribute
cells of unit volume. Find the number of ways to distribute ![]() distinguishable particles (with
distinguishable particles (with
![]() ) within
) within ![]() cells, such that
each cell may be either empty or filled up by only one particle. How would
your answer be modified for indistinguishable particles?
cells, such that
each cell may be either empty or filled up by only one particle. How would
your answer be modified for indistinguishable particles?

![]() . To each equilibrium position, there corresponds a unique
displaced position. Given the number
. To each equilibrium position, there corresponds a unique
displaced position. Given the number ![]() of atoms, and the total energy
of atoms, and the total energy ![]() ,
calculate the number of accessible microscopic states of this system.
,
calculate the number of accessible microscopic states of this system.