


Next: About this document ...
Chapter 1 - Answers to selected exercises
1. Obtain the probability of adding up six points if we toss three distinct
dice.
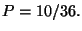 2. Consider a binomial distribution for a one-dimensional random walk, with
2. Consider a binomial distribution for a one-dimensional random walk, with 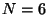 ,
, 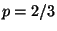 , and
, and 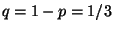 .
a. Draw a graph of
.
a. Draw a graph of
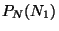 versus
versus 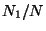 .
b. Use the values of
.
b. Use the values of
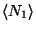 and
and
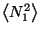 to obtain the corresponding Gaussian distribution,
to obtain the corresponding Gaussian distribution,
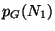 . Draw a graph of
. Draw a graph of
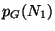 versus
versus 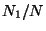 to compare
with the previous result.
c. Repeat items (a) and (b) for
to compare
with the previous result.
c. Repeat items (a) and (b) for 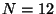 and
and 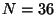 . Are the new answers too
different?
. Are the new answers too
different?
3. Obtain an expression for the third moment of a binomial distribution.
What is the behavior of this moment for large 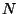 ?
?
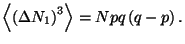 4. Consider an event of probability
4. Consider an event of probability 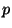 . The probability of
. The probability of 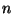 occurrences
of this event out of
occurrences
of this event out of 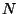 trials is given by the binomial distribution
trials is given by the binomial distribution 
If 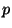 is small (
is small (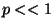 ),
), 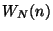 is very small, except for
is very small, except for 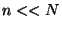 . In
this limit, show that we obtain the Poisson distribution,
. In
this limit, show that we obtain the Poisson distribution,
where
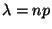 is the mean number of events. Check that
is the mean number of events. Check that
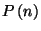 is normalized. Calculate
is normalized. Calculate
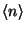 and
and
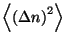 for this Poisson
distribution. Formulate a statistical problem to be solved in terms of this
distribution.
Note that
for this Poisson
distribution. Formulate a statistical problem to be solved in terms of this
distribution.
Note that
![$ \left( 1-p\right) ^{n}=\exp \left[ -pN+...\right] $](img26.gif) , and
, and
![$ N!/\left(
N-n\right) !=\exp \left[ n\ln N+...\right] $](img27.gif) , for
, for 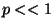 and
and 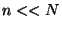 .
Also,we have
.
Also,we have
Therefore,
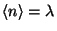 and
and
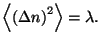 5. Consider an experiment with
5. Consider an experiment with 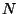 equally likely outcomes, involving two
events
equally likely outcomes, involving two
events 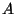 and
and 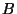 . Let
. Let 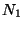 be the number of events in which
be the number of events in which 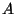 occurs,
but not
occurs,
but not 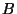 ;
; 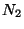 be the number of events in which
be the number of events in which 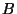 occurs, but not
occurs, but not 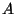 ;
; 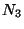 be the number of events in which both
be the number of events in which both 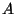 and
and 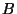 occur; and
occur; and 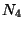 be the number of events in which neither
be the number of events in which neither 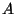 nor
nor 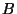 occur.
(a) Check that
occur.
(a) Check that
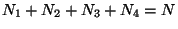 .
(b) Check that
.
(b) Check that
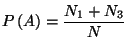 and and 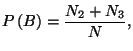 |
|
where
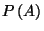 and
and
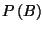 are the probabilities of
occurrence of
are the probabilities of
occurrence of 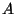 and
and 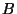 , respectively.
(c) Calculate the probability
, respectively.
(c) Calculate the probability
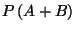 of occurrence of either
of occurrence of either 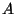 or
or 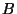 .
(d) Calculate the probability
.
(d) Calculate the probability
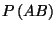 of occurrence of both
of occurrence of both 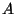 and
and 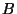 .
(e) Calculate the conditional probability
.
(e) Calculate the conditional probability
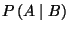 that
that 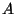 occurs given that
occurs given that 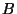 occurs.
(f) Calculate the conditional probability
occurs.
(f) Calculate the conditional probability
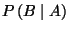 that
that 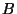 occurs given that
occurs given that 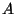 occurs.
(g)Show that
occurs.
(g)Show that
and
(h) Considering a third event 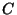 , show that
, show that
which is an expression of Bayes' theorem.
6. A random variable 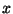 is associated with the probability density
is associated with the probability density
for
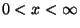 .
(a) Find the mean value
.
(a) Find the mean value
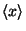 .
(b) Two values
.
(b) Two values 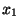 and
and 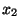 are chosen independently. Find
are chosen independently. Find
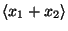 and
and
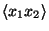 .
(c) What is the probability distribution of the random variable
.
(c) What is the probability distribution of the random variable
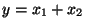 ?
(a)
?
(a)
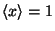 ; (b)
; (b)
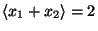 and
and
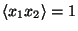 ;
(c) Note that
;
(c) Note that
To obtain this result, it is enough to use an ntegral representation of the 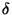 -function (see Appendix) and perform the integrations.
-function (see Appendix) and perform the integrations.
7. Consider a random walk in one dimension. After 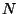 steps from the origin,
the position is given by
steps from the origin,
the position is given by
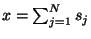 , where
, where
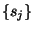 is a set of independent, identically distributed, random
variables, given by the probability distribution
is a set of independent, identically distributed, random
variables, given by the probability distribution
where 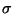 and
and 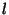 are positive constants. After
are positive constants. After 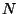 steps, what is the
average displacement from the origin? What is the standard deviation of the
random variable
steps, what is the
average displacement from the origin? What is the standard deviation of the
random variable 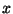 ? In the large
? In the large 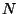 limit, what is the form of the
Gaussian distribution associated with this problem?
limit, what is the form of the
Gaussian distribution associated with this problem?
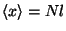 ;
;
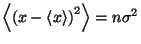 ;
;
8. Consider again problem 7, with a distribution
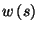 of the
Lorentzian form
of the
Lorentzian form
with 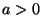 . Obtain an expression for the probability distribution associated
with the random variable
. Obtain an expression for the probability distribution associated
with the random variable 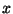 . Is it possible to write a Gaussian
approximation for large
. Is it possible to write a Gaussian
approximation for large 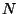 ? Why?
Now we should be careful, as
? Why?
Now we should be careful, as
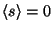 , but
, but
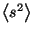 diverges! The Lorentzian form does not
obey the conditions of validity of the central limit theorem.
diverges! The Lorentzian form does not
obey the conditions of validity of the central limit theorem.



Next: About this document ...
Jairo da Silva
2001-03-12
![]() ?
?
![]() 4. Consider an event of probability
4. Consider an event of probability ![]() . The probability of
. The probability of ![]() occurrences
of this event out of
occurrences
of this event out of ![]() trials is given by the binomial distribution
trials is given by the binomial distribution ![]()
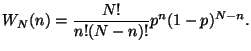
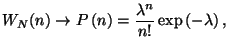
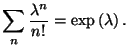
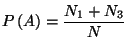 and
and 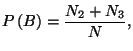
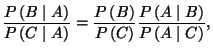
![]() is associated with the probability density
is associated with the probability density
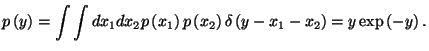
![]() steps from the origin,
the position is given by
steps from the origin,
the position is given by
![]() , where
, where
![]() is a set of independent, identically distributed, random
variables, given by the probability distribution
is a set of independent, identically distributed, random
variables, given by the probability distribution
![$\displaystyle w(s)=\left( 2\pi \sigma ^{2}\right) ^{-1/2}\exp \left[ -\frac{\left(
s-l\right) ^{2}}{2\sigma ^{2}}\right] ,$](img66.gif)
![$\displaystyle p_{G}\left( x\right) =\left( 2\pi N\sigma ^{2}\right) ^{-1/2}\exp \left[ -
\frac{\left( x-Nl\right) ^{2}}{2N\sigma ^{2}}\right] .$](img71.gif)
![]() of the
Lorentzian form
of the
Lorentzian form